Kewen Peng

ACTIVELY SEEKING FULL-TIME JOBS!

More details on LinkedIN

I am a Ph.D. student in Department of Computer Science at North Carolina State University under the supervision of Dr. Tim Menzies. I joined the Real-world Artificial Intelligence for Software Engineering (RAISE) lab in 2019.

Before coming to NC State, I earned my B.S. degree of Computer Science from Wake Forest University in 2019, where I also earned my B.A. degree of Mathematics.

Email /  Resume

Research

My research interests include using data mining and artificial intelligence methods to solve real-world problems in software engineering field. I am also interested in making AI models more explainable and actionable. My recent research includes (a) exploring the disagreement problem in multi-objective optimization, and (b) interpretable mitigation of bias in ML software. This May I'm presenting my paper at the 45th International Conference on Software Engineering. Please check out my presentation here!

Projects
NLP & Information Retrival
  • Persona and Knowledge Empowered Conversational AI: Designed and implemented a social-chat conversational model, which generates personalized answers to a user’s question based on the user’s persona information and knowledge base. Implemented (a) hierarchical cross attention, and (b) STS-based grounding component to locate context-relevant candidates. Implemented in PyTorch, experimented with BART and GPT-2, the new approach reaches comparable performance to baseline methods and obtained 20% reduction in training and inference cost.
    • Fairness Enhancement & Explanation Generation
  • Detect and explain bias: Developed predictive models, measuring fairness in confidential data using various fairness metrics, and generating explanations for better understanding the internal state of black box models. Experiment results shows that our model can better reflect the extent of bias/fairness in the given data space, measured by different fairness metrics.
  • Bias mitigation: Prototyped a novel model that can not only achieve better group fairness than prior state-of-the-art methods, but also ensure perfect individual fairness as well as procedural justice. Moreover, our approach has trivial damage on the predictive power of the original model.
    • Search-based Software Engineering
  • Multi-objective configuration optimization: Explore potential model disagreement in model-based optimization. Propose a dimension reduction approach that generate a hyper-space for mapping configurations while preserving the domination relationship among them. The result shows that our simplification can achieve optimizer models of zero disagreement (measured by Kendall's t test), while maintaining on-par performance measured by generational distance .
    • Selected Publication
    FairMask: Better Fairness via Model-Based Rebalancing of Protected Attributes
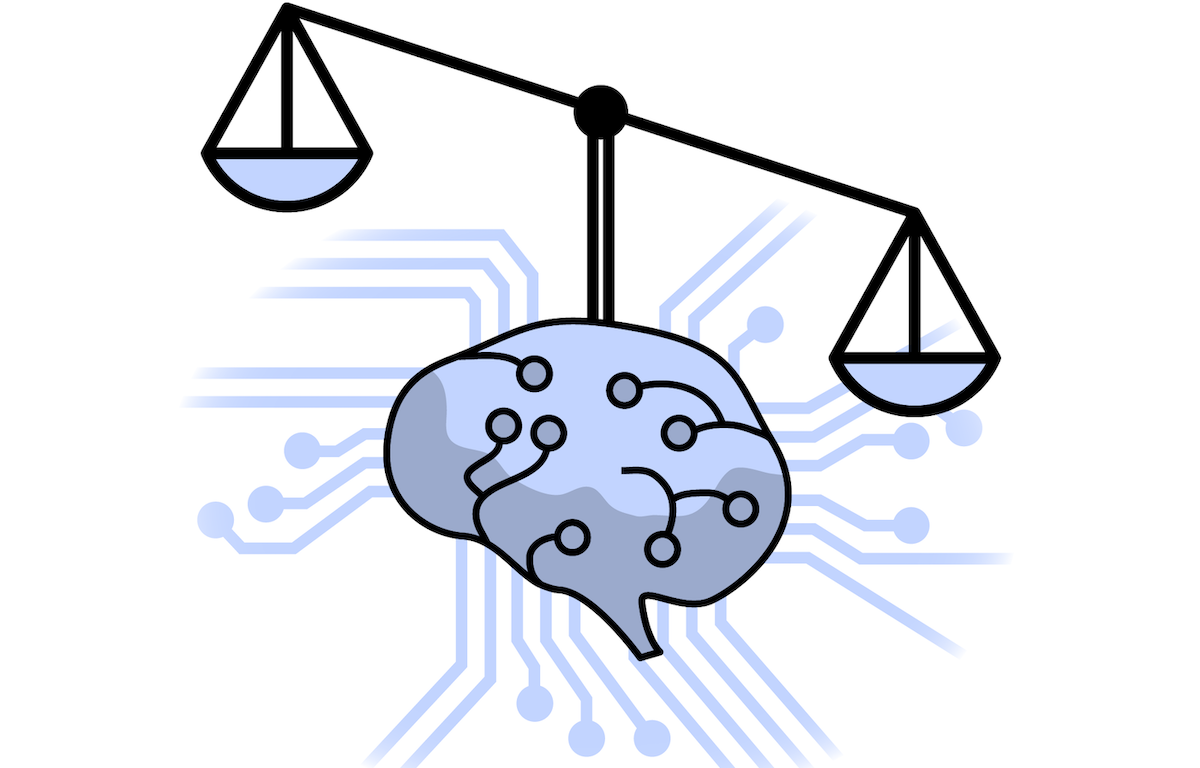
    Kewen Peng, Joymallya Chakraborty, Tim Menzies
    Transactions on Software Engineering (TSE), 2023 (accepted)

    We propose FairMask, a model-based extrapolation method that is capable of both mitigating bias and explaining the cause. By reasoning and masking the protected attribute, FairMask minimizes the performance loss while achieving perfect procedural justice.

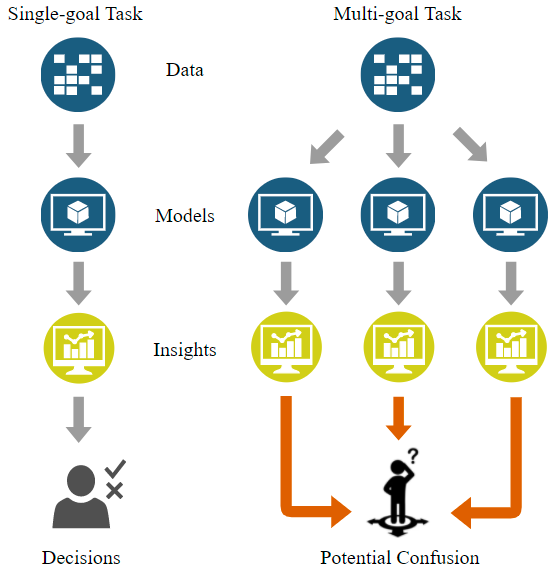
    VEER: Enhancing the Interpretability of Model-based Optimizations
    Kewen Peng, Christian Kaltenecker, Norbert Siegmund, Sven Apel, Tim Menzies
    Empirical Software Engineering (EMSE), 2023 (accepted)

    We propose a dimension reduction method called VEER that builds a useful one-dimensional approximation to the original N-objective space. For our largest problem, optimizing with VEER finds as good or better optimizations with zero model disagreements, three orders of magnitude faster.

    Making fair ML software using trustworthy explanation
    Joymallya Chakraborty, Kewen Peng, Tim Menzies
    IEEE/ACM International Conference on Automated Software Engineering (ASE), 2020 (accepted)

    Our work concentrates on finding shortcomings of current bias measures and explanation methods. We show how our proposed method based on K nearest neighbors can overcome those shortcomings and find the underlying bias of black box models. Our results are more trustworthy and helpful for the practitioners.

    Defect Reduction Planning (using TimeLIME)
    Kewen Peng, Tim Menzies
    Transactions on Software Engineering (TSE), 2021 (accepted)

    Software comes in releases. An implausible change to software is something that has never been changed in prior releases. When planning how to reduce defects, it is better to use plausible changes, i.e., changes with some precedence in the prior releases. TimeLIME is a more effective and actionable way to plan defect reduction using sensitivity analysis.

    On the Noether Bound for Noncommutative Rings
    Luigi Ferraro, Ellen Kirkman, W Frank Moore, Kewen Peng
    Proceedings of the AMS (PAMS), 2020 (accepted)

    We present two noncommutative algebras over a field of characteristic zero that each posses a family of actions by cyclic groups of order 2n , represented in n x n matrices, requiring generators of degree 3n.

    TA Experience
    CSC216 Programming Concepts - Java
    CSC510 Software Engineering